ここでは車両モデルの最も基本となる物理モデルの解説をする
変速時のイナーシャトルクについては割愛。また「トルク→加速度の変換」&「走行抵抗の扱い」も割愛。ねじり振動の勉強になる記事ですよ。
当該アプリは
ver0
ver1
体系
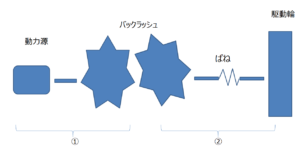
以下に示すような「①動力源」と「②駆動輪」の2つの箇所の運動方程式を個別に立てていく。
体系図
動力源①の物理式
動力源と歯車を含めたイナーシャをI1、動力源にかかるトルクをT1、①の角速度をw1、①から②へ伝わるトルクをT12とすると
I1w1d=T1-T12
ここで添え字のdは微分を表す。
駆動輪②の物理式
駆動輪のイナーシャをI2、②の角速度をw2とすると
I2w2d=T12
ここで添え字のdは微分を表す。
シャフトのねじりT12について
こちらはばねのねじりで構成される。また歯車が介在するため、ガタつき不感帯が存在する。そのため以下のように条件で式が分かれる。Kはねじり剛性[Nm/rad]、Cは減衰係数[Nm/(rad/s)]。単位は要注意だ。あと符号がどっちになるかもちゃんと意識するように。①のほうが早いときはT12は正になる!
T12=K×∬(w1d-w2d)dt+C×∫(w1d-w2d)dt ーーーガタ詰まってるとき
T12=0 ーーーガタ詰まっていないとき
離散化について
下の手順でよいかと。もっと凝りたい方はルンゲクッタなどで解いてください。
- 初期の角度差を設定
- T12を計算
- ①でw1dを計算。T1は入力のため、未知数はw1dのみ
- ②でw2dを計算。未知数はw2dのみ
- 上記の3,4の手順で求まるw1d,w2dから速度差、角度差を計算
- 手順2に戻る
それぞれの式をみてわかること
- ガタ量が大きいほどガタが詰まるまでに∫(w1d-w2d)dtが増えるため、T12がステップ的に作用
- I1が大きいほどw1の変化が緩慢になるため、ガタ詰め以降のK×∬(w1d-w2d)dt+C×∫(w1d-w2d)dtのピーク時の値が増す
改良の余地
- 駆動輪以降の抵抗を加える
- 駆動輪の上に車体をつける
おわりに
あまりこのガタ詰め時(バックラッシュが詰まる時)のインパクトショックを取り扱っている文献が見当たらないため、参考になればと思う。

